La compression Web

Alors que vous lisez ces lignes, des millions de requêtes HTTP sont échangées sur le web.
Des millions de clients s’affairent à décompresser leurs contenus, tandis que des millions de serveurs, de leur côté, les ont compressés.
Et ça, pour nous, Hubert et Antoine, c’est fascinant.
Nous avons donc passé pas mal de temps à étudier ce sujet afin de vous en partager l’essentiel ici.
Attention, nous risquons de glisser quelques discrètes références au jeu du Scrabble. Pourquoi ? Vous verrez bien !
Un peu de lexique
Avant de creuser le sujet, il est important de bien comprendre les termes utilisés.
Quand on parle de compression, le monde se divise en deux catégories :
- La compression sans perte de données.
- La compression avec perte de données.
En général, on associe la compression avec perte de données à des formats d’image ou d’audio/vidéo : JPEG, MP3 ou MPEG.
Cependant, sur le web, on retrouve également de la compression avec perte de données sur des fichiers JavaScript, CSS ou encore HTML.
Dans ces cas-là, on parle de minification.
Prenons un exemple simple avec ce code JavaScript :
export function add(firstNumber, secondNumber) {
return firstNumber + secondNumber;
}
// Recursive FTW!
export function factorial(number) {
if (number === 0) {
return 1;
}
return number * factorial(number - 1);
}Pour l'instant, le fichier fait 228 octets. Le minifieur1 va le transformer car il connaît la syntaxe du langage.
Il va retirer les points-virgules et les commentaires qui n’affectent pas le comportement du code.
export function add(firstNumber, secondNumber) {
return firstNumber + secondNumber;
}
export function factorial(number) {
if (number === 0) return 1;
return number * factorial(number - 1);
}On gagne déjà quelques octets en passant à 203 octets.
Mais le minifieur va aller bien plus loin que ça, en ajustant la syntaxe JavaScript de manière bien plus fine.
Par exemple ici il va :
- transformer un
ifen une ternaire2 ; - supprimer les sauts de ligne ;
- supprimer les espaces inutiles.
Pour arriver à un résultat le plus petit possible sans changer le fonctionnement du code.
export function add(f,s){return f+s}export function factorial(n){return n===0?1:n*factorial(n-1)}Et ça, c'est un exemple assez simple des transformations qu'un minifieur moderne est capable de réaliser.
Une fois qu'on a atteint les limites de ce qu'on peut faire avec la minification, on applique alors de la compression.
Le compresseur, l'outil dont on va se servir pour compresser le contenu du fichier sans perte, ne connaît pas la syntaxe du langage du fichier qu'il va compresser.
Il agit directement sur les octets du fichier, en utilisant des algorithmes de compression.
Dans l'exemple précédent, en appliquant la minification, nous sommes passés à 98 octets, et en appliquant la compression, nous obtenons un fichier de 89 octets.
Belle économie, non ?
Nous vous l'accordons, cet exemple n'est pas très représentatif. Voyons maintenant des exemples plus significatifs.
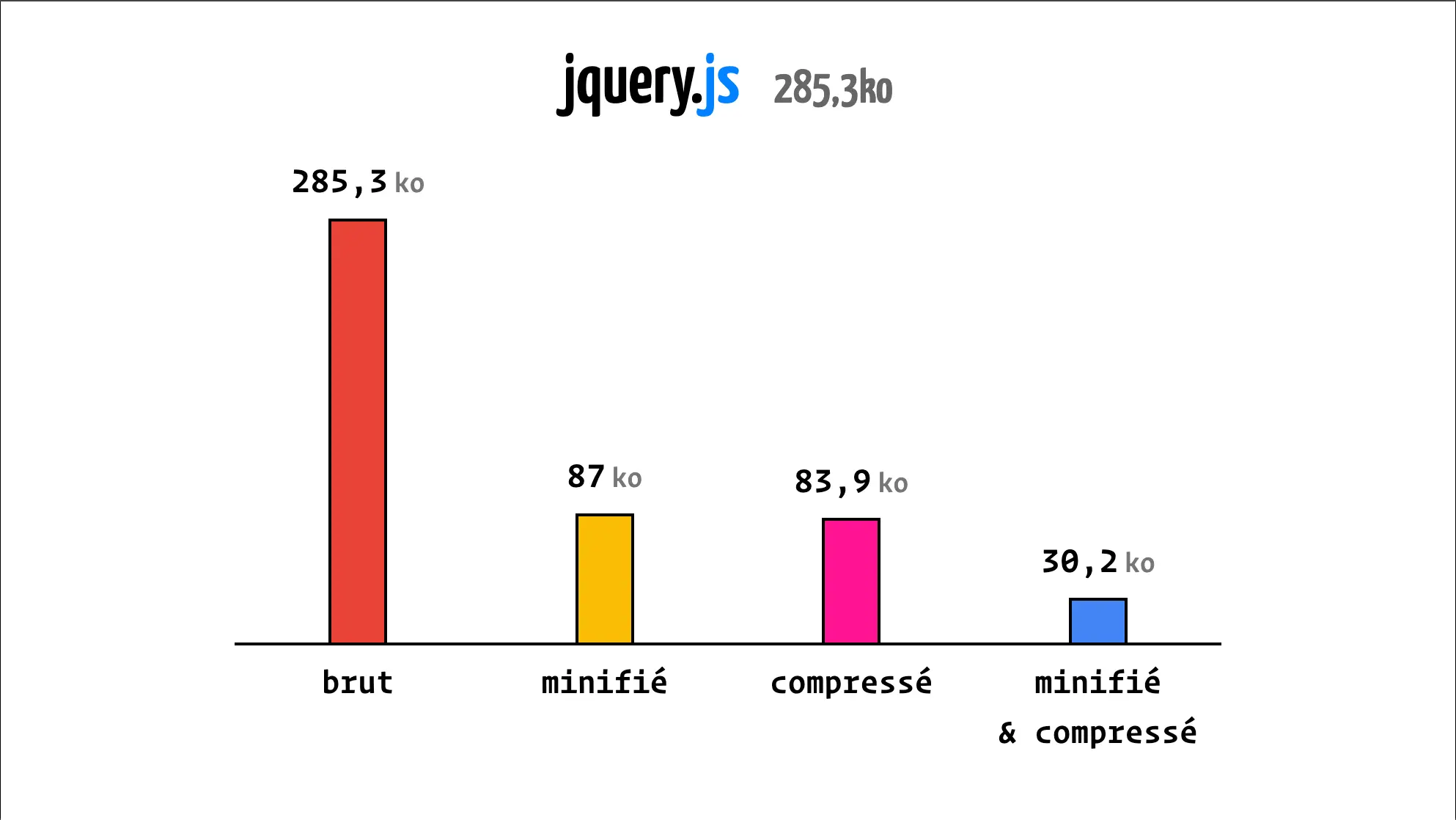
Prenons le cas de jQuery, un fichier de 285,3 Ko non minifié et non compressé.
On constate que, sur un fichier plus conséquent, la minification et la compression apportent des gains bien plus importants.
Ici, entre la minification et la compression, on gagne 90% sur le poids brut du fichier.
La minification à elle seule permet de réduire de 69% le poids du fichier. En effet, dans le fichier brut de jQuery, il y a beaucoup de commentaires.
Ces logiques ne s'appliquent heureusement pas qu'au JavaScript.
Prenons maintenant un fichier HTML conséquent : la documentation complète d'Hibernate en un seul fichier.
Oui, ça existe !
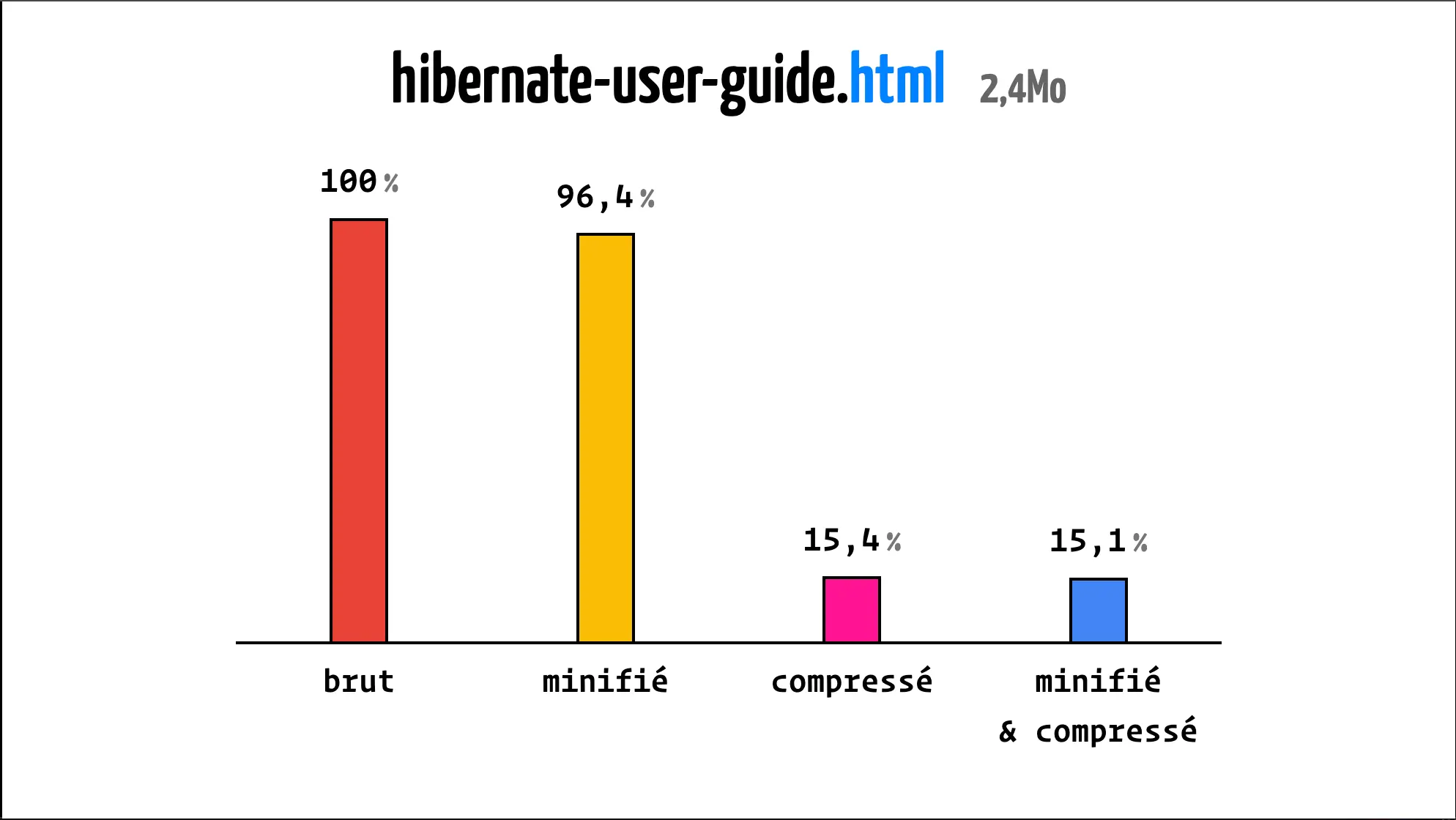
Dans ce cas-là, on peut observer que la minification apporte peu. En effet, il y a peu à minifier dans un fichier HTML.
Sur les graphiques précédents, on comprend que la minification apporte de bons résultats.
Cela dépend quand même du format du fichier, sur un fichier HTML il y a souvent peu de code inutile à supprimer.
Cependant, ce qu'il faut retenir et noter, c'est que la compression apporte toujours de meilleurs résulats quand elle est précédée d'une étape de minification.
Ok, la compression et la minification permettent de réduire la taille des fichiers, mais quel impact cela a-t-il pour les utilisateurices ?
Est-ce que ça a un impact sur la vitesse de chargement des pages ?
Prenons une page web au hasard, la page Wikipédia du Scrabble.
Une page web, c'est un ensemble de requêtes en cascade.
Le chargement et l'analyse de la page déclenche en cascade le chargement et l'analyse d'autres ressources, etc.
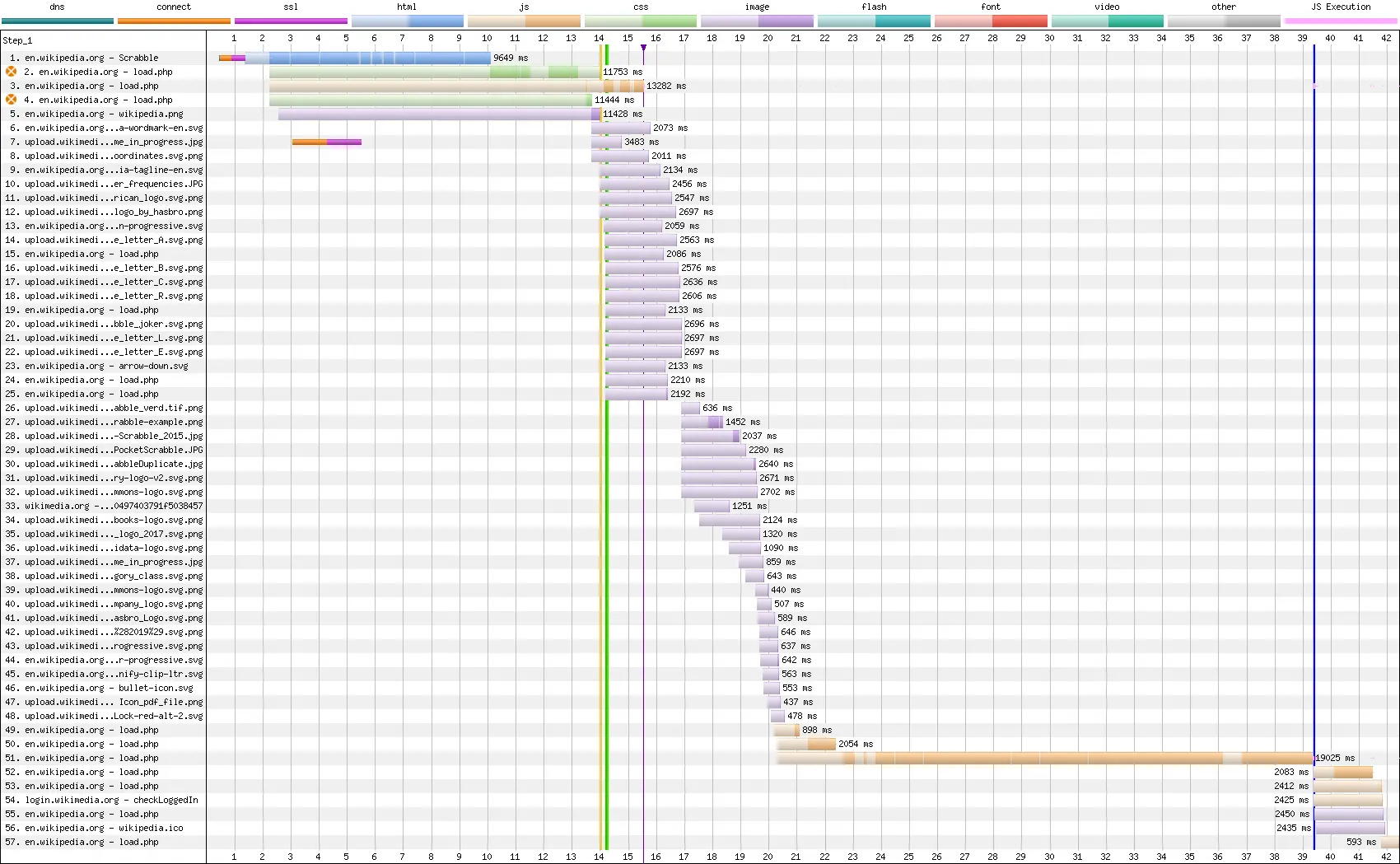
Comparons donc en 3G, en 4G et sans limitation de réseau le temps de chargement de la page wikipedia du Scrabble avec et sans compression. Nous avons utilisé WebPageTest pour réaliser ces tests comparatifs.
Vous allez nous dire : « Oui mais en 2024 tout le monde sait qu'il faut compresser ses fichiers.
Alors ! »
Vous connaissez l'Almanach du Web ?
C'est une étude qui permet de voir l'évolution des pratiques sur le web.
Regardons les résultats de l'étude de 2022 sur la compression.
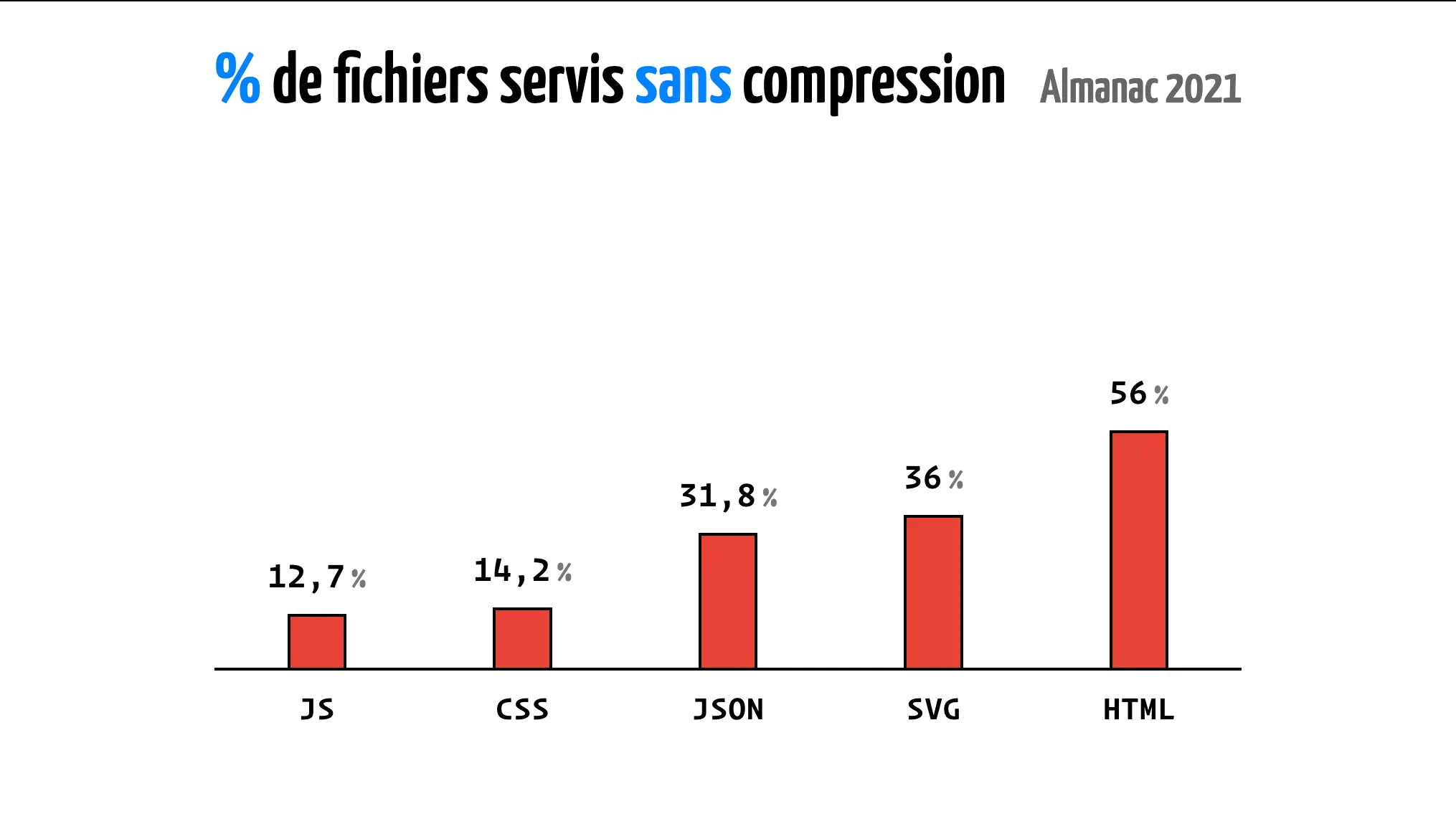
Clairement, ça nous a fait très peur.
Et là, on ne parle que du web public accessible à tout le monde, et uniquement des page d'accueil de sites, pas des intranets ou des applications internes.
Bon, on peut se rassurer, l'étude de 2024 vient de sortir et les chiffres sont meilleurs.
Seulement 11% des fichiers HTML ne sont pas compressés alors qu'en 2022 c'était 56%.
Retenez donc : vérifier que la compression est en place est encore nécessaire en 2024.
Dans les tuyaux
Ok, maintenant qu'on sait qu'il faut compresser, comment ça marche dans le navigateur ?
Alors déjà, retenez que la compression n'est pas obligatoire.
C'est le navigateur qui envoie un en-tête Accept-Encoding dans la requête HTTP pour indiquer au serveur qu'il est capable de décompresser le contenu.
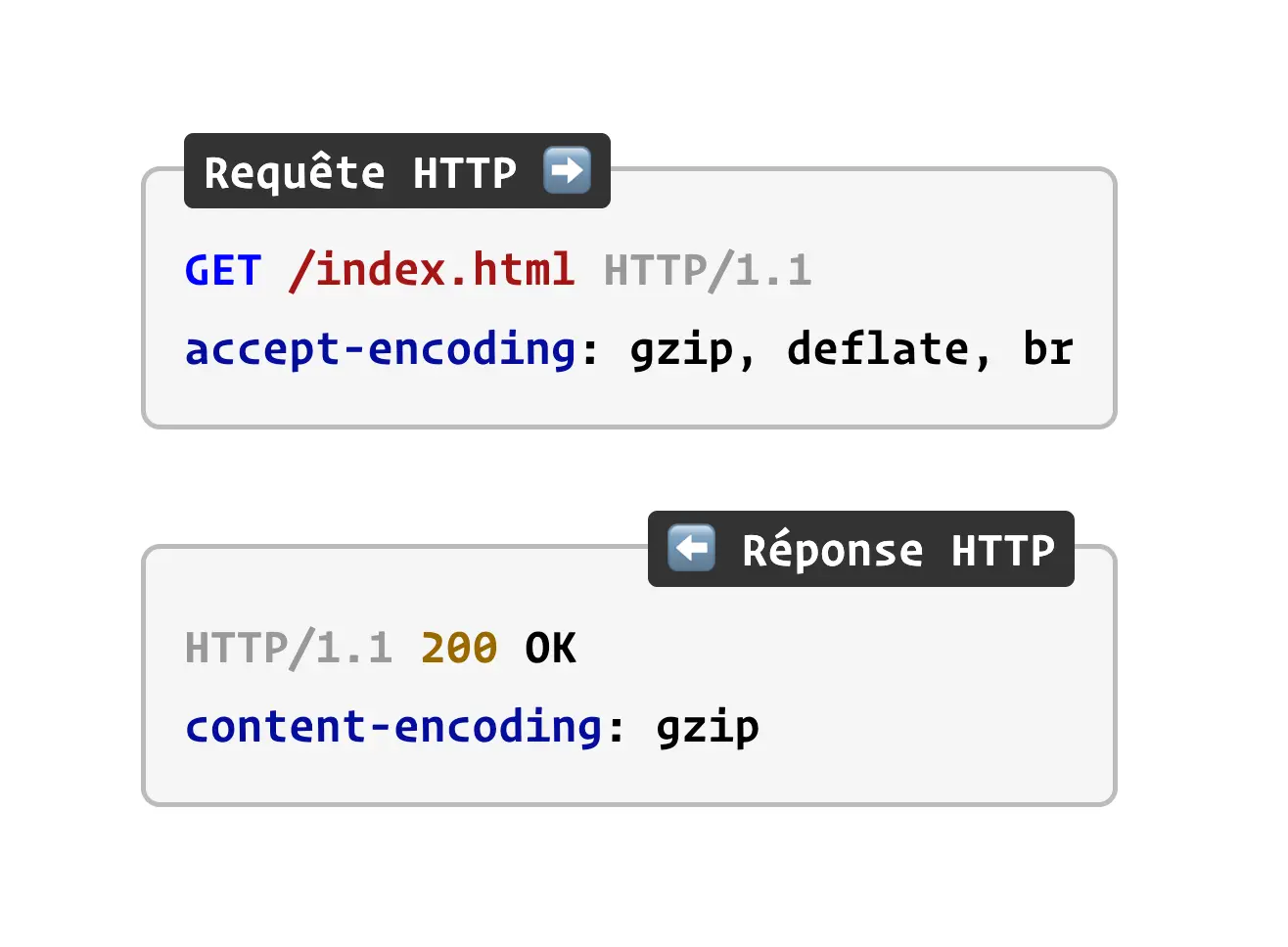
Grâce à cet en-tête, le serveur va pouvoir choisir de compresser ou non le contenu tout en retournant l'en-tête Content-Encoding, pour indiquer au navigateur le type de compression utilisé.
Bien configuré, un serveur web utilisera toujours un format supporté par le navigateur qui l'interroge.
Le site web caniuse.com, qui permet de voir la compatibilité des technologies web dans les navigateurs, a un affichage très spécifique pour le support de gzip.
En effet, le support de gzip est tellement répandu qu'il est considéré comme acquis.
C'est cool, non ? C'est pas tout !
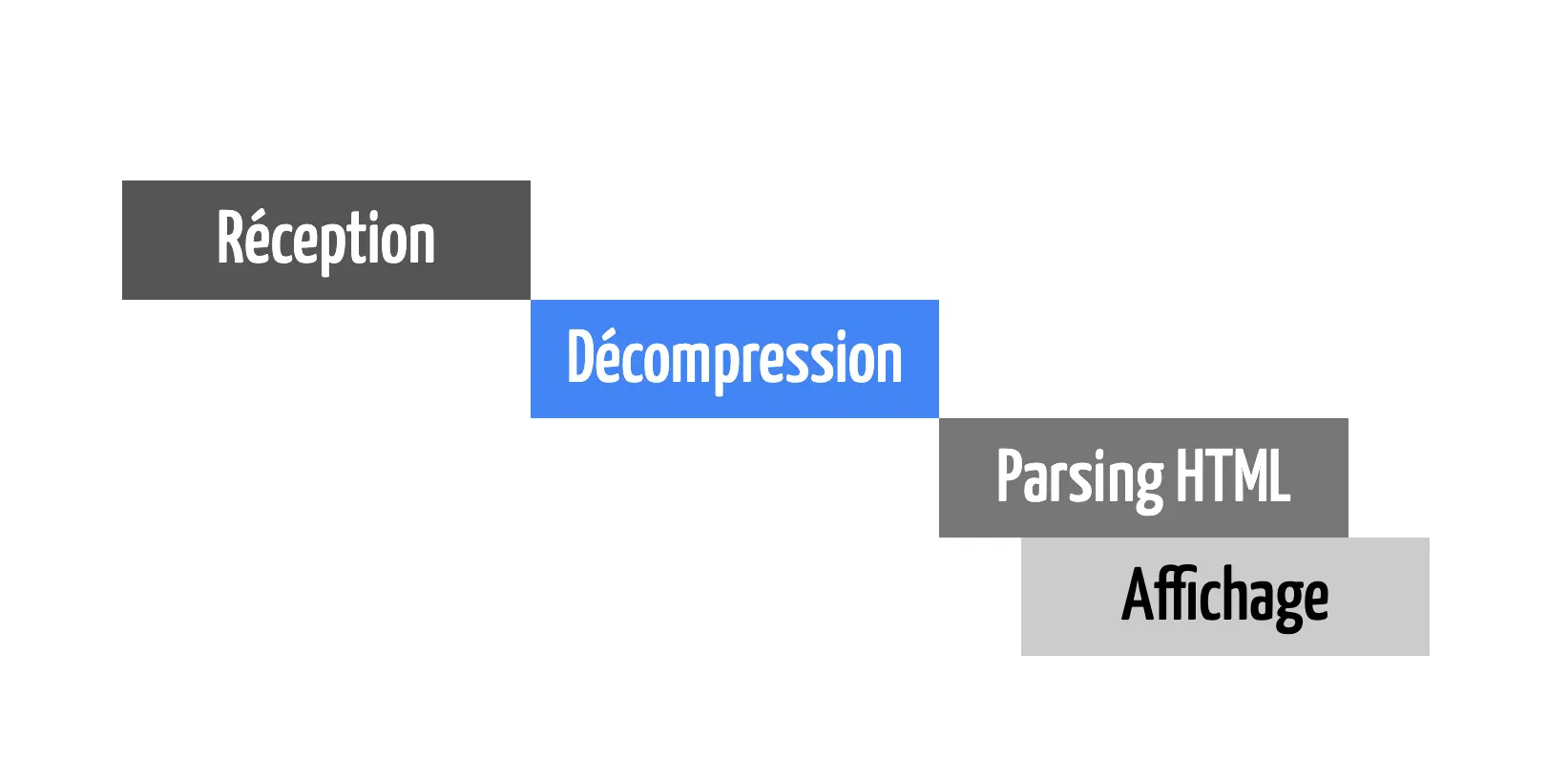
Au départ, on pensait naïvement que la compression et la décompression étaient une étape bloquante entre le serveur et le navigateur.
Même si cette étape était bloquante, on gagnait du temps car le fichier était plus petit.
Si on schématise ce qu'on imaginait, on pensait que le serveur compressait tout le contenu, puis l'envoyait au navigateur qui décompressait tout le contenu et l'affichait.
Ce n'est pas comme ça que le web fonctionne, nos navigateurs peuvent commencer à afficher l'HTML qu'ils reçoivent sans attendre d'avoir reçu le document en entier.
Pour le prouver, on a donc fait un site web qui contient l'intégralité des œuvre de Sherlock Holmes (toutes les nouvelles et les romans).
Oui la page est lourde, mais c'est justement le but, cela permet de mieux se rendre compte du chargement et de l'affichage progressif.
Et puis bon, on vient peut-être de créer la meilleure façon de lire Sherlock Holmes en ligne !
On a même activé la compression pour voir ce que ça donne.
Dans cette vidéo, on voit que le contenu est affiché progressivement, même si le téléchargement du fichier n'est terminé.
Et cela, même si le serveur compresse le contenu à la volée, on observe que le DOM se construit de manière progressive.
Dans cette situation, on pourrait même imaginer que le serveur n'a pas encore compressé les derniers octets du fichier HTML que le navigateur a déjà décompressé et affiché le début de la page.
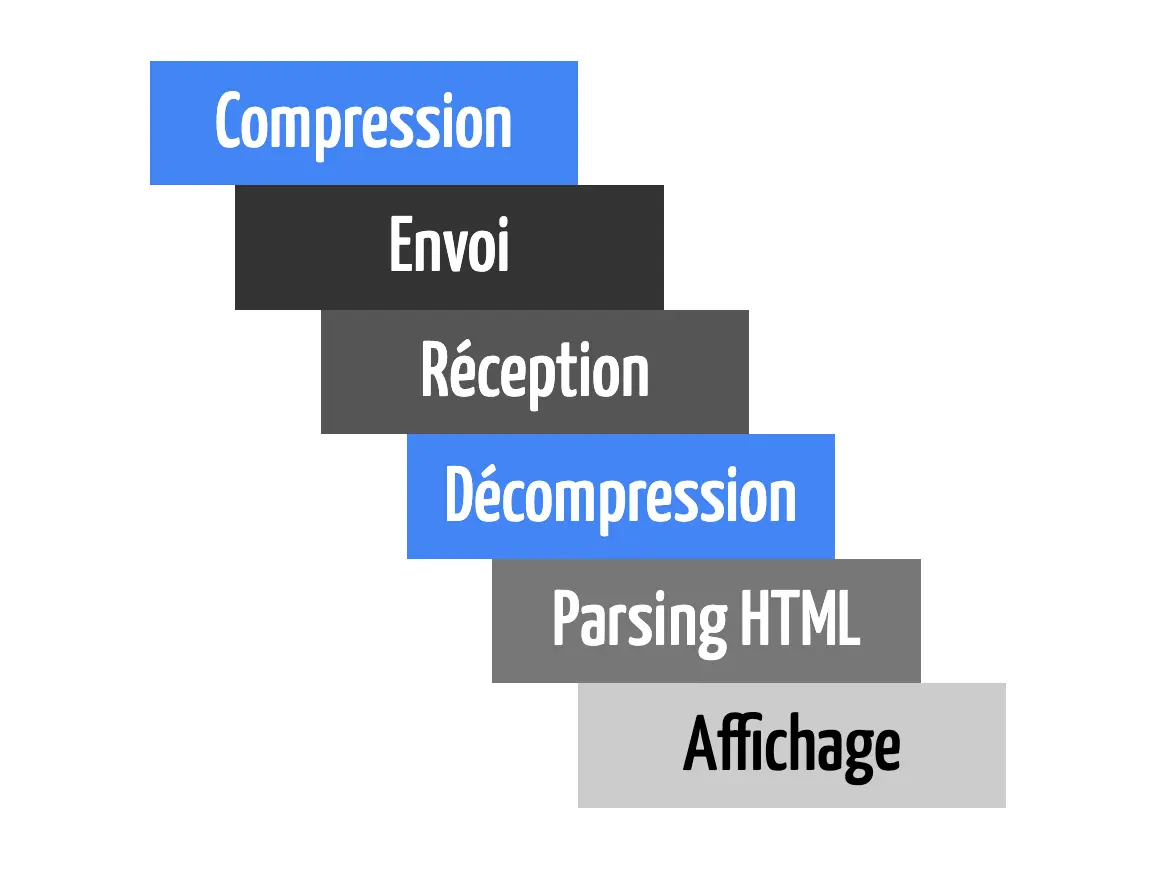
Retenez donc que la compression et la décompression n'interrompent pas le flux.
Un peu d'histoire
Bon, tout cela n'est pas nouveau, la compression web avec gzip on la retrouve définie dans une RFC de 1992.
Jean-Loup Gailly et Mark Adler posèrent les bases de la compression telle qu'on la connait depuis plus de trente ans maintenant.
Pour se faire, ils se sont basés de travaux de Phil Katz sur PKZIP, qui a défini dans une RFC dédiée, le format de fichier zip que vous connaissez certainement.

Mais Phil Katz n'a pas construit la format zip à partir de rien, il a repris des travaux bien plus anciens.
Reprenant les travaux d'Abraham Lempel et de Jacob Ziv datant de 1977, il réutilise l'algorithme LZ77 comme base.
Enfin, pour encoder de manière optimisée, Phil Katz a également pu se baser sur les travaux de David Huffman datant de 1952 avec son codage de Huffman.
La compression dans le web est un bel exemple de cascade de découvertes et des impacts de la recherche fondamentale dans notre société.
Plus de trente ans nous séparent maintenant de la publication de gzip, et plus de quarante ans séparent cette publication des travaux initiaux de David Huffman.
Le web sans la compression serait terriblement différent si ces travaux n'avaient pas été menés, on pourrait même imaginer que la révolution qu'il a apporté aurait été limitée.
Comprenons le codage de Huffman
Après cette délicieuse tranche d'histoire, on va essayer de comprendre un peu mieux le codage de Huffman.
David Huffman, en 1952, se dit «En codant les caractères qui apparaissent le plus souvent avec peu de bits, et en codant les caractères qui apparaissent le moins souvent avec beaucoup de bits, en moyenne, on devrait réduire le nombre de total de bits et gagner de la place. »
Vous n'avez rien compris ? C'est normal. En fait, c'est un peu comme le Scrabble.
Vous connaissez ce jeu où on tire des tuiles avec des lettres et où il faut former des mots ?
Les lettres les plus courantes ont un faible nombre de points, alors que les lettres les moins courantes ont un nombre de points plus élevé.
C'est un peu la même logique.

Si on est capable de générer un code binaire pour chaque caractère.
Les caractères les plus fréquents auront un code binaire court, et les caractères les moins fréquents auront un code binaire long.
Et dans les faits, ça marche terriblement bien.
David Huffman

Ce qu'il faut savoir, c'est que David Huffman a 26 ans quand il publie cela.
Alors qu'il étudie au MIT, dans la même classe que Claude Shannon, son professeur lui donne un choix de publier un article ou de passer un examen. David choisi de faire un article scientifique.
Il invente et publie le codage de Huffman ainsi que l'algorithme qui permet de le déterminer.
Il prouve également que mathématiquement, son codage est le plus optimal possible.
Principes de l'algorithme
Si on reprend le mot COMPRESSION et qu'on applique le codage de Huffman.
La première étape sera de compter les fréquences de chacunes des lettres, c'est à dire, combien de fois elles sont répétées dans le message.

On va ensuite construire un arbre binaire en appliquant le principe suivant : on fusionne les branches de lettres avec les fréquences les plus basses en créant un nouveau nœud qui portera comme fréquence la somme des fréquences des deux branches fusionnées.
On va d'abord regrouper dans notre exemple, les lettres I et N formant un nœud de fréquence deux. Puis R et E de la même manière, M et P, puis il ne reste que C comme lettre, avec une fréquence de un. On la regroupe avec la lettre S de fréquence deux formant un nœud de fréquence trois. On répète l'opération jusqu'à avoir un seul nœud en haut de l'arbre.
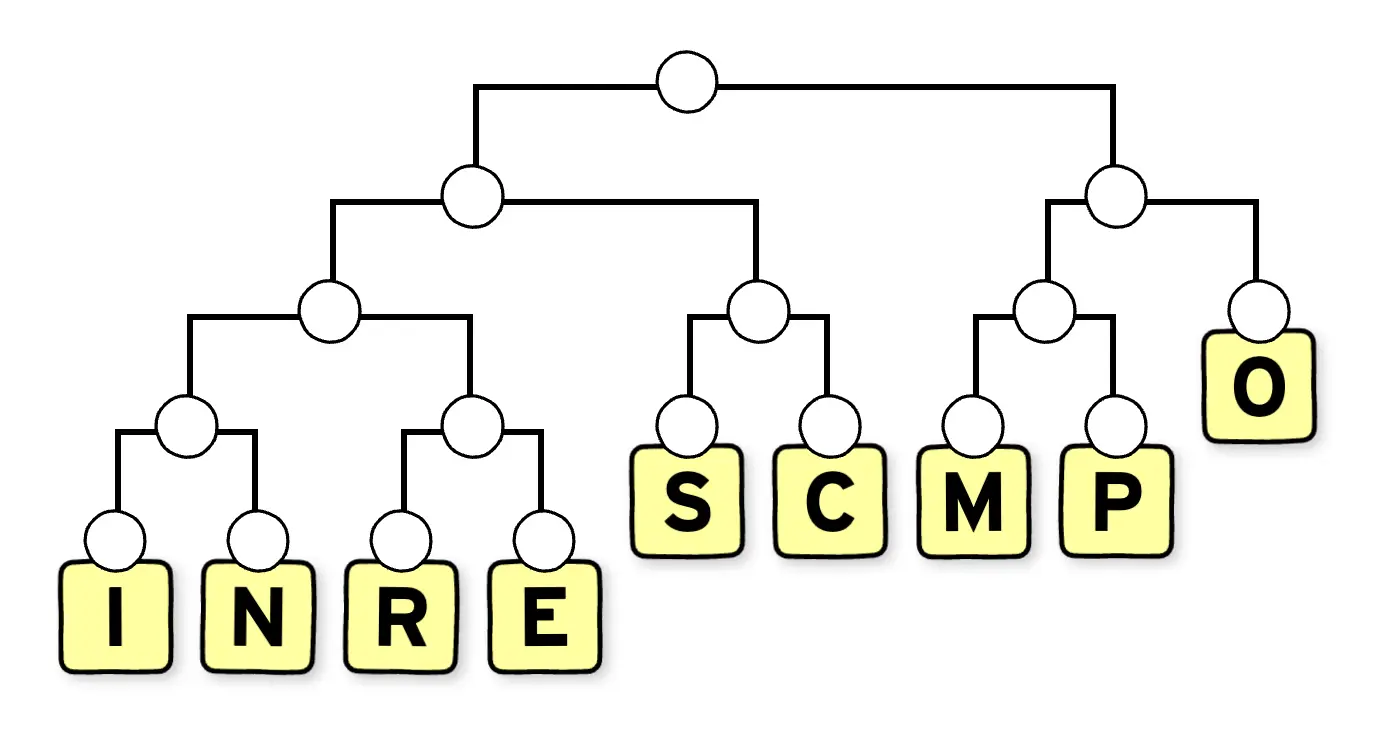
Il faut ensuite affecter à chaque branche de l'arbre binaire, soit le bit 0 ou 1.
On obtient alors un code binaire unique pour chacune des lettres en descendant l'arbre du noeud principal jusqu'à la lettre.
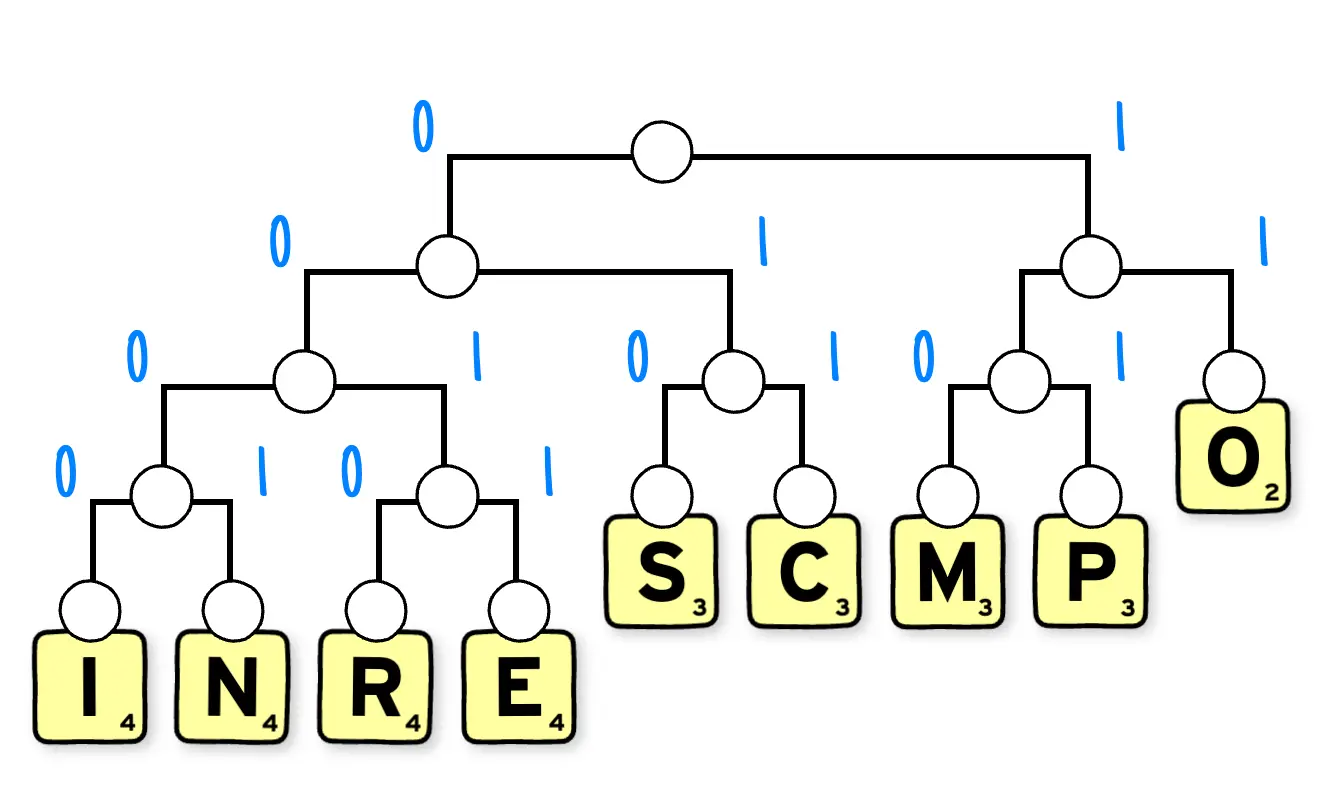
On obtient alors pour chaque lettre un code binaire unique dont la longueur est fortement liée à la fréquence de cette lettre dans le message.
| Lettre | Code binaire |
|---|---|
| I | 0000 |
| N | 0001 |
| R | 0010 |
| E | 0011 |
| S | 010 |
| C | 011 |
| M | 100 |
| P | 101 |
| O | 11 |
Imaginons qu'il nous soit nécessaire de coder chaque lettre du mot avec un octet. Il nous faudrait 88 bits pour coder le mot compression. Avec le codage de Huffman généré ici, seulement 35 bits seraient nécessaires.

Bien évidemment, il faudra trouver un moyen de partager ou connaître l'arbre binaire à la compression et à la décompression.
Si on reprend l'image du Scrabble, appliquer le codage de Huffman sur un mot, c'est comme avoir une case lettre compte moins.
LZ77 c'est quoi ?
Bon en 1977, alors que Carlos sortait son célèbre Big Bisou, Abraham Lempel et Jacob Ziv publient un article sur un algorithme de compression sans perte.
Ils se disent qu'au vue de la teneur des messages qu'on échange numériquement à l'époque, on peut sûrement faire mieux que simplement appliquer un codage de Huffman.
Prenons cet exemple de texte :
On peut tromper une personne mille fois.
On peut tromper mille personnes une fois.
Mais on ne peut pas tromper mille personnes, mille fois.
— Extrait de la cité de la peur
Clairement, dans ce message on se répète beaucoup, et on ne répète pas uniquement des lettres, on répète des motifs complexes.
L'idée de Lempel et Ziv c'est de dire, si on a déjà vu un motif, on peut le remplacer par une étiquette qui indique la distance et la longueur de ce motif plus tôt dans le message.
Voyons donc comment ça marche avec un exemple, prenons le gateau préféré d'Antoine : le mille-feuille.
Appliquons l'algorithme de LZ77 à ce délicieux dessert.

L'algorithme LZ77 va lire le message avec une fenêtre de lecture de trois caractères.
Au début, pour la première lettre M, il va regarder si il a déjà vu le triplet M,I,L plus tôt dans le message.
Ici, on vient tout juste de commencer donc non.
LZ77 va donc directement retourner le symbole M.

Il en est de même jusqu'au deuxième I.
Ici, le triplet I,L,L a déjà été vu plus tôt dans le message. On peut donc remplacer le symbole I par ce qu'on va appeler une étiquette. Cette étiquette aura une longueur de trois car nous pouvons remplacer les trois symboles I,L,L. Maintenant, LZ77 va calculer la distance de cette étiquette. C'est à dire, de combien de symboles il faut remonter dans le message pour retrouver le même triplet. L'algorithme vérifie ensuite si le motif répété est plus long que la fenêtre de trois symboles. Ici c'est le cas, l'étiquette peut remplacer quatre symboles.

Quelques autres découvertes sur ce système d'étiquettes :

- Les étiquettes peuvent avoir une longueur supérieure à leur distance, si ce motif s'applique plusieurs fois d'affilée.
- Le système d'étiquette est très simple algorithmiquement à décoder, une seule passe sur le message est nécessaire.
En inventant un système d'encodage efficace pour ces références, on peut réduire la taille du message.
Il faut cependant trouver un moyen simple et compact d'encoder ces étiquettes.
Et concrètement gzip, ça marche comment ?
Alors en fait, un an après avoir créé l'algorithme LZ77, Lempel et Ziv créent... l'algorithme LZ78.
En fait, il existe une vraie famille d'algorithmes LZ : LZ77, LZ78, LZSS, LZW, etc.
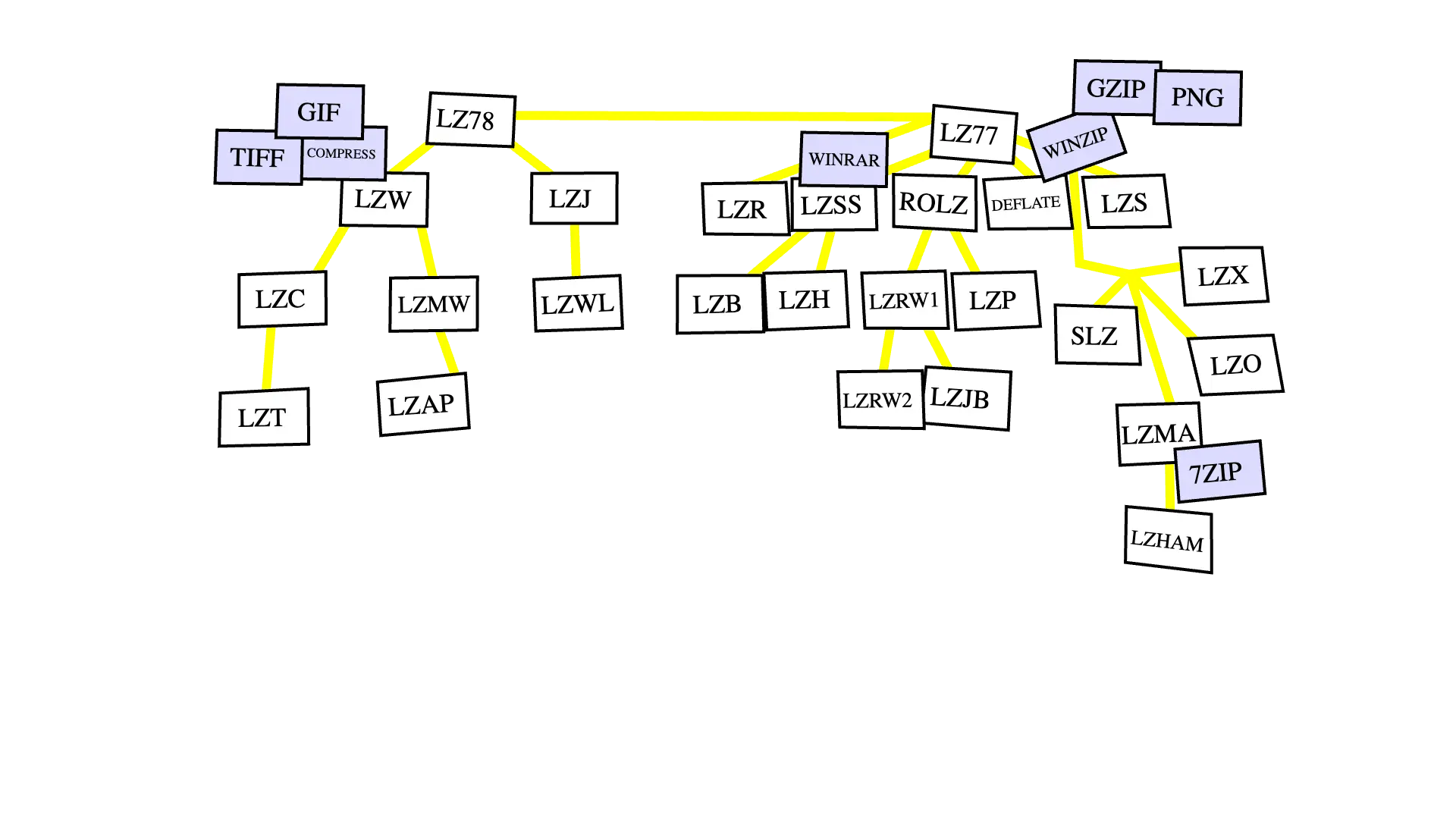
Vous allez retrouver l'alternative LZW dans les formats de fichiers GIF et TIFF.
LZSS dans Winrar, LZMA dans 7zip.
D'ailleurs, vous avez peut-être déjà entendu parler de LZMA cette année.
Si ces sujets vous intéressent, nous vous conseillons la vidéo de Colt McAnlis.
Bon, pour en revenir à gzip, revenons donc à Phil Katz.
En 1990, il se dit: « Si à mon fichier, j'applique l'algorithme LZ77 pour obtenir des étiquettes et des symboles, puis le codage de Huffman, je vais obtenir un fichier plus petit. »
Il décide d'appeler cela Deflate, et référence ça dans la RFC 1951.

En rajoutant des en-têtes et des pieds de page, il obtient le format de fichier zip.

Quelques années plus tard, Jean-Loup Gailly et Mark Adler se disent: « Et si on appliquait ça au web ? »
Ils créent alors la zlib et formalise une nouvelle RFC qui se base également sur Deflate mais avec des en-têtes et des pieds de page différents de ce qu'à proposé Phil Katz.
On retrouve cela en détail dans la RFC 1952.

Bon, nous n'irons pas plus dans le détail dans cet article, mais si le contenu des blocs Deflate vous intéresse et si vous avez un peu de temps, disons vingt heures, la liste de lecture de vidéos de Bill Bird sur YouTube vous permettrait de creuser ce sujet.
À la recherche du pouillème
Définissons ensemble ce qu'est un pouillème.
C'est déjà, scientifiquement, une unité de mesure qui veut dire « à peu près pas beaucoup ».
Au vu de la quantité d'échanges sur le web, si on arrive à gagner un pouillème supplémentaire grâce à la compression, il y a énormément d'économies à faire.
Donc clairement, les gros consommateurs de bande passante, les géants du web, cherchent à gagner des pouillèmes.
C'est la cas de Cloudflare par exemple, qui a son propre fork de la zlib.
Quand gzip est apparu, il y avait déjà la possibilité de choisir entre plusieurs niveaux de compression.
De 1 à 9, ces niveaux permettent d'avoir une compression plus ou moins forte du fichier.
En jouant sur quelques paramètres, et contre quelques millisecondes de calculs supplémentaires, gzip va alors trouver des motifs plus complexes et donc plus efficaces.
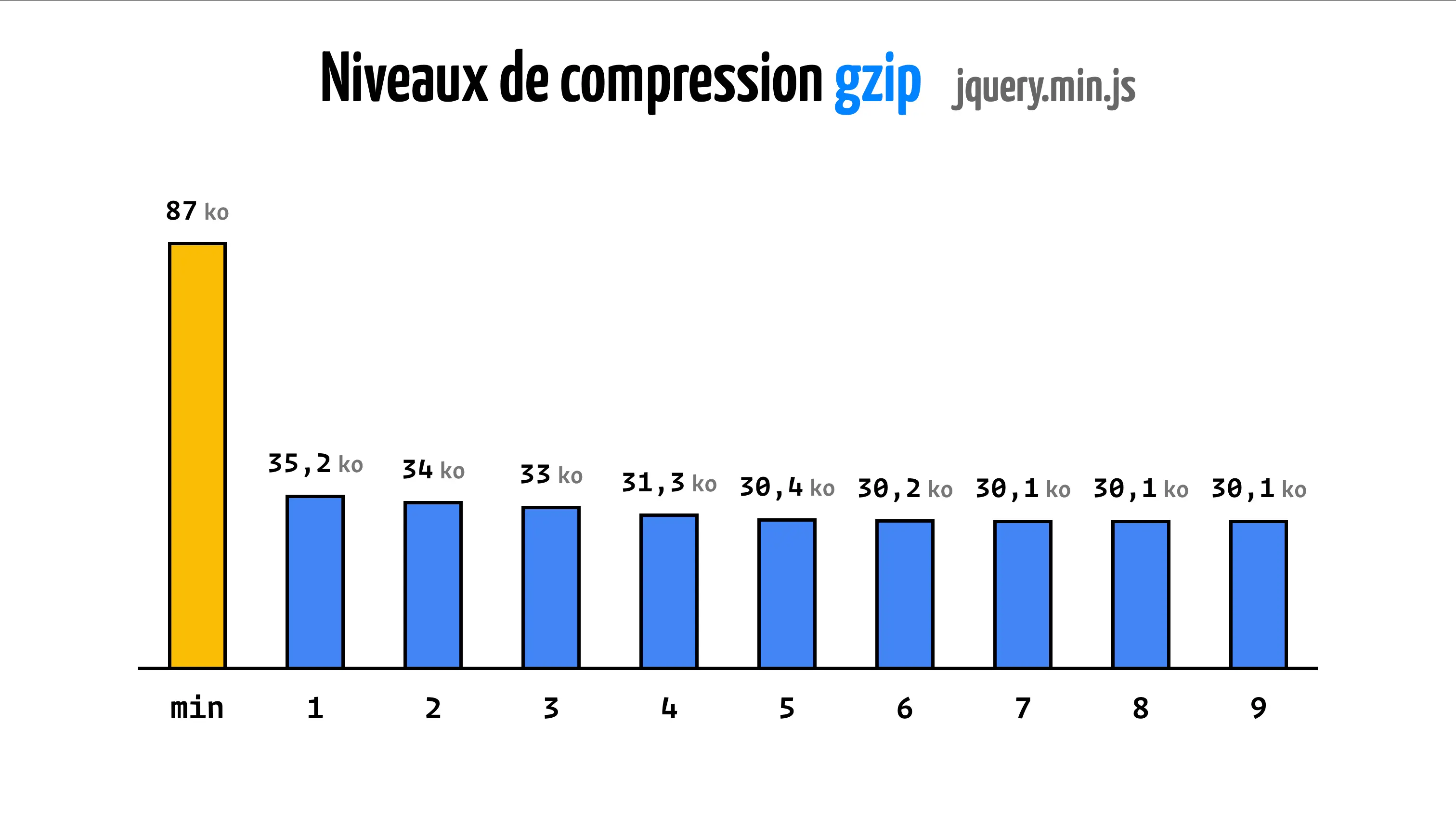
Dans les années 2010, Google se dit : « Et si on faisait mieux que gzip tout en gardant le format de fichier gzip ? »
Ils créent alors Zopfli qui est clairement une implémentation de gzip qui brute-force 3 la recherche de motifs dans l'algo LZ.
On gagne quelques pouillèmes, mais on ajoute beaucoup de temps de calcul. Dans les faits, en appliquant Zopfli avec le niveau 9 de gzip sur ce même fichier, on peut le réduire à 29,2 Ko au lieu de 30,1 Ko.
Quelques années plus tard, les mêmes ingénieurs de chez Google se disent plusieurs choses :
- le format de fichier gzip est un peu vieux et on pourrait faire mieux pour gagner quelques octets ;
- dans le web, on connaît à peu près la structure des fichiers qu'on manipule. On sait par exemple qu'un fichier HTML va avoir une balise
htmlet qu'une feuille de style CSS va certainement avoir des attributs commemargin.
Ils créent alors Brotli et le spécifient dans la RFC 7932.
Brotli triche, il possède à la compression et à la décompression un énorme dictionnaire dans lequel il peut référencer des étiquettes avec LZ77.
13 504 mots sont dans ce dictionnaire auquel il peut appliquer 121 transformations (comme lowercase, uppercase, etc), ce qui nous donne 1 633 984 possibilités.
C'est énorme !
Et en 2024, Brotli est supporté par tous les navigateurs modernes.
Dans le dictionnaire de Brotli, il y a des mots comme data, code, ou bien encore des motifs plus longs comme <!DOCTYPE html><html. On y trouve principalement de l'anglais, mais aussi de l'espagnol, du chinois, de l'hindi et du russe. Et comme vous l'avez vu avec notre dernier exemple, on y trouve aussi du HTML, du CSS et du JavaScript. L'idée derrière ce dictionnaire est très pragmatique, dans le web on connaît déjà une partie de ce qui va être transféré.
Comparons maintenant l'efficacité de ces trois algorithmes sur un fichier JavaScript comme jquery.min.js avec les différents niveaux.
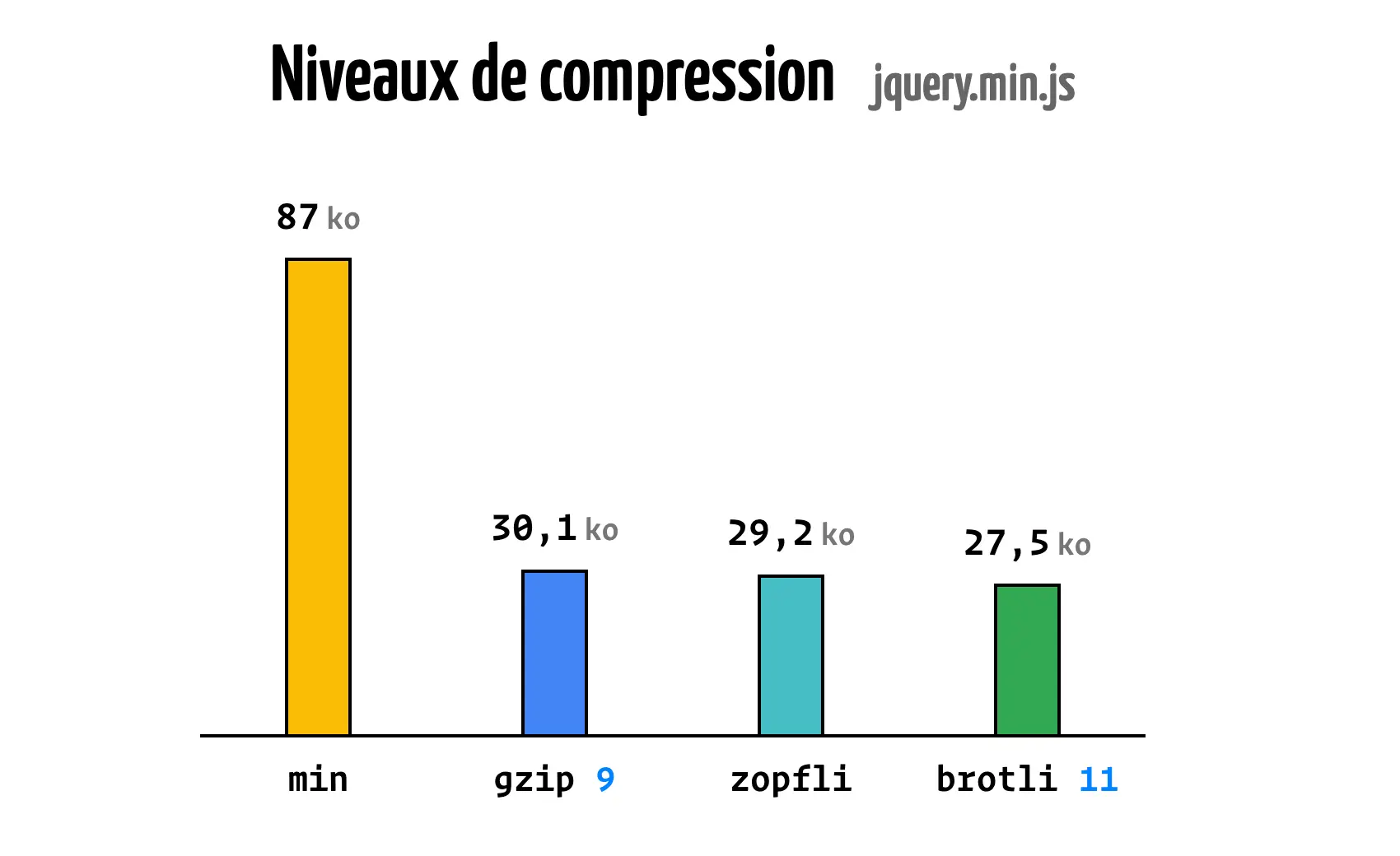
Retenez donc que la compression dans le web, ça marche mieux avec brotli.
Maintenant, comparons les performances et le temps nécessaire à la compression et la décompression pour chaque niveau.
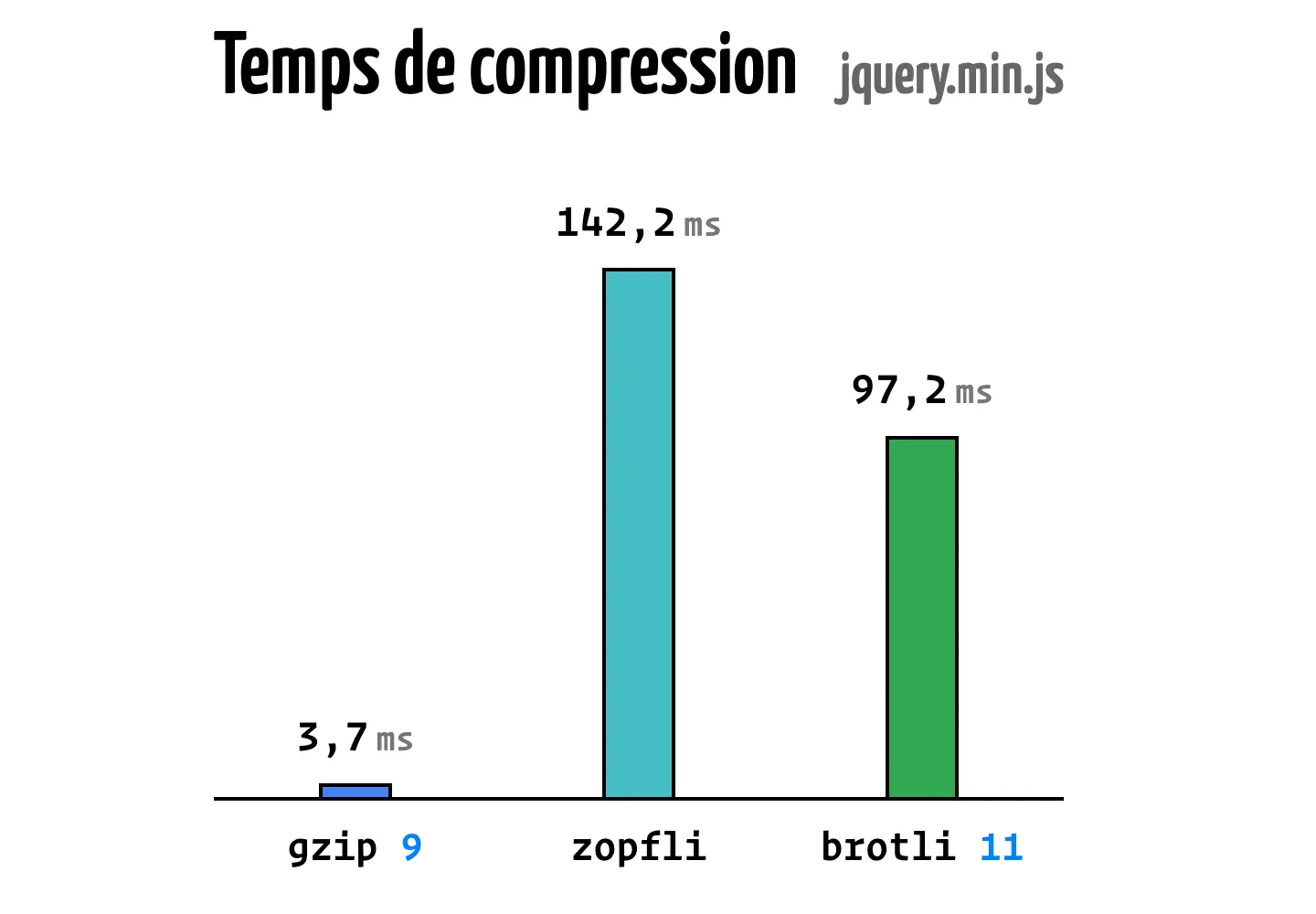
L'Almanac du Web vous propose donc une recommendation claire pour choisir le niveau de compression à utiliser.
- Les fichiers statiques doivent être compressés une seule fois à la génération avec les meilleurs niveaux de Brotli et Gzip ou Zopfli.
- Les fichiers dynamiques doivent être compressés à la volée avec un niveau de compression plus faible pour ne pas ralentir le serveur.
Il est donc recommandé d'appliquer dans cette situation un niveau de cinq avec Brotli et de six avec Gzip.
Enfin, retenez que le niveau de compression n'a pas d'impact sur la décompression. Un fichier compressé en niveau 11 avec Brotli mettra un temps équivalent à être décompressé en comparant au même fichier compressé avec gzip en niveau 1.

Ne sont-ils pas beaux ces petits chats ? — Hubert
Bon, pourquoi nous avons décidé de mettre cette photo des chats d'Hubert ?
Cette image est un JPEG, un format d'image qui utilise la compression avec perte de données.
Voici les résultats de la compression de cette image avec Brotli, Gzip et Zopfli.
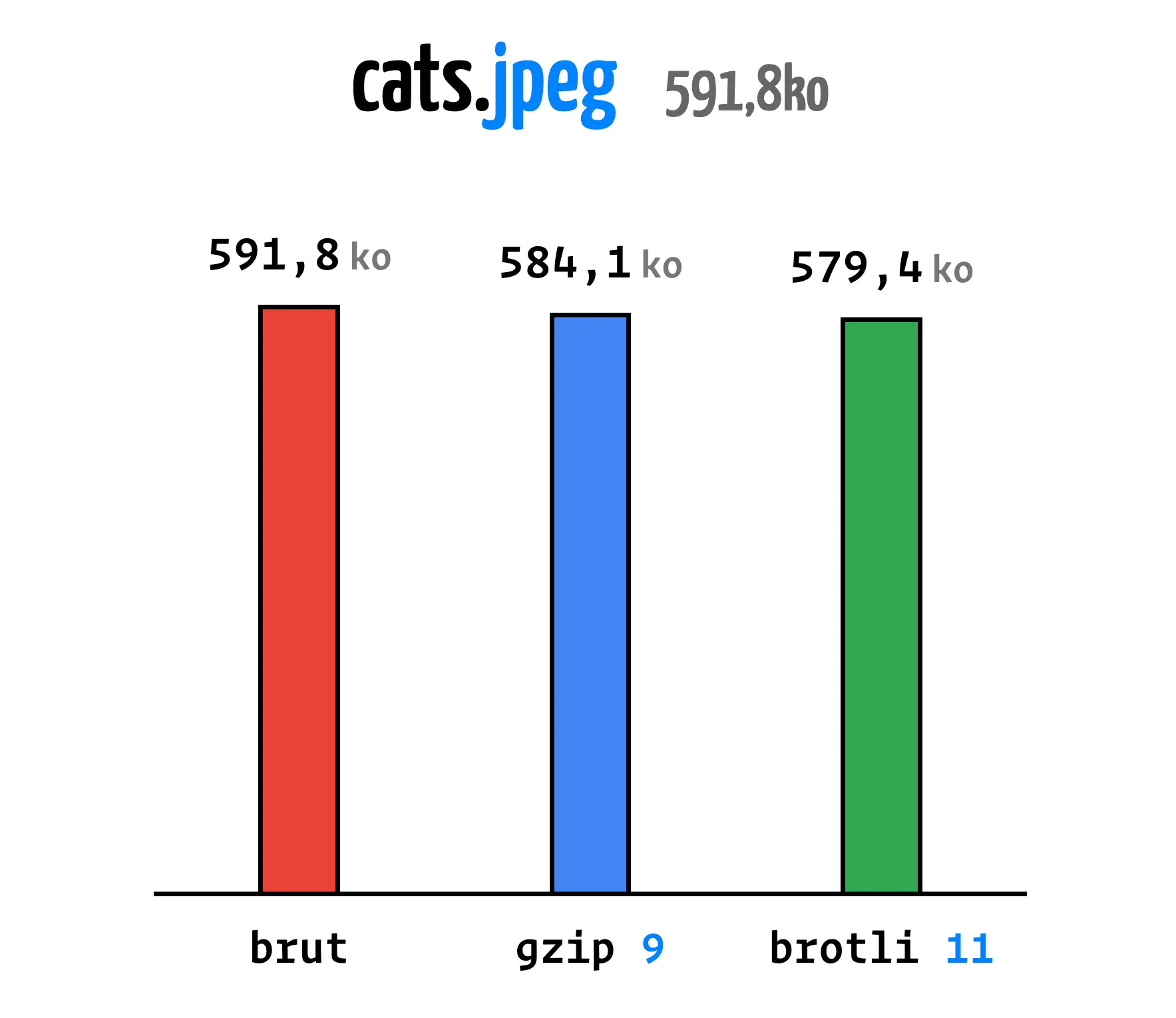
Clairement, ce n'est pas efficace, la compression avec perte de données a déjà fait le travail, il n'y a rien à enlever.
Vous pourriez nous reprocher de dire une évidence, mais l'Almanach du Web nous rappelle que 3,27% des JPEG sont servis compressés avec gzip dans le web.
Pour autant, certains fichiers binaires ne sont pas compressés par défaut.
Il faut donc appliquer de la compression sans perte pour les servir.
Les formats font/otf, font/ttf, image/bmp et image/x-icon sont des exemples de fichiers binaires qui ne sont pas compressés par défaut.
On peut également citer le format WASM qui est souvent oublié dans la configuration des fichiers compressés.
Pourtant, les binaires WASM sont souvent très lourds et peuvent bénéficier de la compression.
Au delà du poullième
Contrairement à ce qu'on pourrait croire, la compression sans perte n'est pas un sujet à l'arrêt ou bien un sujet qui ne connaît pas de nouvelles évolutions. Nous aurions pu également vous parler de sujets chauds et des avancées récentes. Cependant, cet article étant déjà bien long, nous vous proposons si le sujet vous passionne autant que nous, de poursuivre avec ces quelques thématiques :
- une implémentation multi cœurs de gzip nommée pigz par Mark Adler. ;
- le support récent de l'algorithme de Meta nommé Zstandard par Meta ;
- une nouvelle spécification pour introduire des dictionnaires partagés entre le navigateur et le serveur, pour gagner encore plus de poids.
Conclusion
Dans cet article, nous avons essayé de faire le tour de ce qui nous paraît essentiel pour comprendre la compression dans le monde du web.
Bon, nous avons aussi inséré discrètement quelques références au Scrabble.
Retenez donc ces neuf rappels et principes :
- La compression va de pair avec la minification.
- La compression est encore nécessaire en 2024.
- La compression est native au fonctionnement du web.
- La compression n'interrompt pas le flux.
- L'algorithme de Huffman, c'est un peu comme lettre compte moins.
- L'algorithme LZ77 réduit le poids des motifs répétitifs complexes par leur remplacement par des étiquettes. C'est mot compte moins.
- La compression dans le web, ça marche mieux avec brotli.
- Les fichiers statiques se compressent une seule fois à la génération.
- La compression n'a pas d'effet sur les fichiers déjà compressés.
Si cet article vous a plu, il existe aussi sous la forme d'une conférence que nous avons donnée dans différentes villes de France. En voici une donnée en 2023 à Nantes.
-
Nom donné à l'outil utilisé pour appliquer de la minification ↩
-
Opération conditionnel simplifiée. ↩
-
Qui explore tout ou partie des solutions possibles. ↩
Il n’est plus possible de laisser un commentaire sur les articles mais la discussion continue :